Our research interests are in experimental quantum optics, nonlinear optics, state reconstruction and measurement, and interferometry. The following describes some of our recent results in more detail.
Entangled photon sources
Much of our research is based on entanglement, one of the quintessential features of quantum mechanics. Entangled photons can be produced through a process called Spontaneous Parametric Down-conversion. Down-conversion is the process of converting a high-energy photon, typically from a laser, into a pair of photons and occurs in nonlinear optical materials such as BBO or KTP. In recent years, it has been discovered that these entangled photons have properties that make them useful for studying quantum communication, computing, and for exploring fundamental questions in quantum physics.
The most famous example of an entangled state is the so-called singlet state of two spin-1/2 particles,
This state has the property that the spins are anti-aligned in any basis. Through measurements of the correlations between spin measurements, it can be used to demonstrate a violation of local realistic descriptions of nature, i.e., a violation of Bell’s inequalities. Using spontaneous parametric down-conversion in properly arranged combinations of nonlinear crystals or interferometers, we can create photon pairs which exhibit the same types of quantum correlations in their polarization degrees of freedom.
Recently, we have developed a source of entangled photons from a periodically-poled nonlinear material. This source is 50 times more efficient at converting laser light into entangled pairs and offers higher quality entanglement as well.
Multi-photon entanglement
Entanglement is not just a property of a pair of particles, it can exist between larger numbers of particles as well. In fact, entanglement gets more complicated and more interesting when more particles are involved.
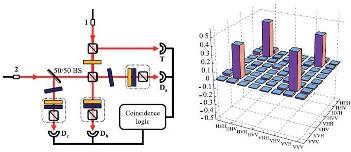
We use high-intensity pulsed lasers to drive multiple synchronized down-conversion sources to produce higher numbers of entangled photons. Using techniques from linear optics quantum computing, we can entangle these pairs together to create more complex multi-photon entangled states.
Recently, we have created 3-photon entangled states called GHZ states with sufficiently high fidelity to test and rule out a nonlocal hidden variable model using Svetlichny’s inequality. We use quantum state tomography to measure the wavefunction of the light and characterize the state.
Further reading: J. Lavoie, R. Kaltenbaek, and K.J. Resch, Experimental violation of Svetlichny’s inequality, New Journal of Physics 11, 073051 (2009).
Quantum-inspired interferometry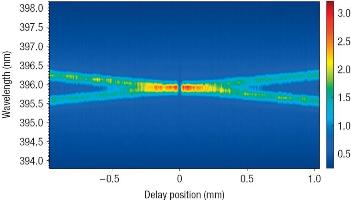 
Interference, the characteristic light and dark regions that occur when two light beams are superposed, is one of the most striking features of both classical and quantum mechanical descriptions of light. It is also an extremely useful phenomenon enabling extremely precise measurements of physical parameters such as length and time. Interference is the basis for some advanced medical imaging techniques, such as optical coherence tomography, which can be used to non-invasively image structures in biological tissue.
Recent work in quantum information science has identified several features of quantum interference which provably outperform the measurement precision allowed with classical interference. Most of these features rely on the quantum mechanical property of entanglement – the quantum phenomenon associated with “spooky action at a distance”. The most prominent example is referred to as phase super-sensitivity, where interference fringes oscillate much faster than the wavelength of light, which could be incorporated into an ultra-sensitive distance measurement device. At the same time, several effects have been observed with entangled quantum systems which offer significant advantages over known classical systems, but have not been proven exclusively quantum effects. Some of these advantages include automatic dispersion cancellation and aberration cancellation, which reduce negative effects of dispersion and distortion, and enhanced resolution which allows the resolution of narrowly spaced features. Many of these effects have been observed in variants of a two-photon quantum interferometer called the Hong-Ou-Mandel interferometer.
We have very recently realized a completely classical interference technique which is capable of producing all of the metrological advantages of the Hong-Ou-Mandel interferometer including: enhanced resolution, phase insensitivity and robustness against loss, and automatic dispersion cancellation. This technique does not require any entanglement at all. We refer to this new technique as chirped-pulse interferometry (CPI) because it relies on stretched, or chirped, ultrafast laser pulses. As an added feature, by using bright classical laser light instead of dim sources of photon pairs, our technique yields signal levels millions of times larger than the quantum device. This advance represents a promising new avenue for classical interferometry and imaging especially in OCT applications.
Further reading: R. Kaltenbaek, J. Lavoie, D.N. Biggerstaff, and K.J. Resch, Quantum-inspired interferometry with chirped laser pulses, Nature Physics 4, 864 (2008); J. Lavoie, R. Kaltenbaek, and K.J. Resch, “Quantum-optical coherence tomography” with classical light, Optics Express 17, 3818 (2009).
Generalized measurements of quantum systems
The classic standard measurement in quantum mechanics is the measurement of spin using a Stern-Gerlach apparatus. In such a device, a beam of randomly oriented spins passing through the device will be split into beams of well-defined spin along the direction of the magnets. The simplest and most important example is the spin-1/2 particles which will either be deflected up or down along the direction of the magnets. In such a standard measurement, the number of different outcomes is equal to the dimension of the state space (for spin-1/2, there are two outcomes for a 2D state space). Furthermore, if we were to repeat the measurement for a second time with the magnets oriented along the same direction, we would get consistent results. That is to say that if we measure the spin to be up along the z direction, and then quickly measure spin along z again, we would find spin up again.
A four-outcome POVM of photon polarization
But these are not the only types of measurements allowed by quantum mechanics. Generalized measurements, which are often referred to by the forgettable acronym POVM (positive operator valued measure), do not need to abide by either of these properties. They can have more outcomes than the dimension of the state space and subsequent applications of the same measurement do not necessarily produce the same outcome.
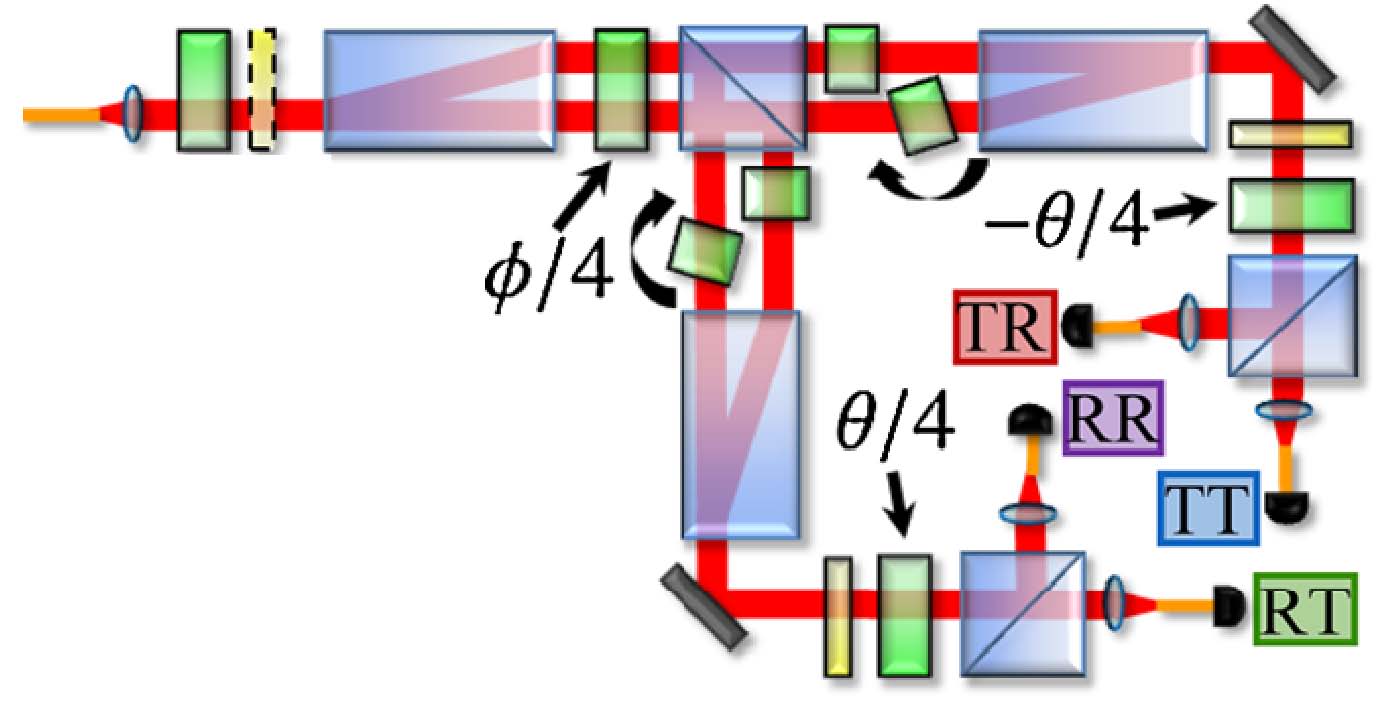
We have recently developed an optical setup capable of implementing a wide array of four-outcome generalized measurements on the polarization of a single photon. It is based on a stable optical interferometer constructed out of beam-displacing calcite blocks.
Interestingly, these measurements have an important application in one-way quantum computing. The original one-way model is based on standard, projective measurements and implements one rotation per qubit in the cluster state. Using our generalized measurement, we can implement two rotations per qubit allowing larger computations on a cluster of fixed size. With the inherently stable construction, we were able to perform over 200 one-way quantum computations and show that these proceed with very high fidelity. We are currently investigating other applications of these types of measurements in quantum information.
Further reading: D. N. Biggerstaff, R. Kaltenbaek, D. R. Hamel, G. Weihs, T. Rudolph, and K. J. Resch, Cluster-state quantum computing enhanced by high-fidelity generalized measurements, Physical Review Letters 103, 240509 (2009).