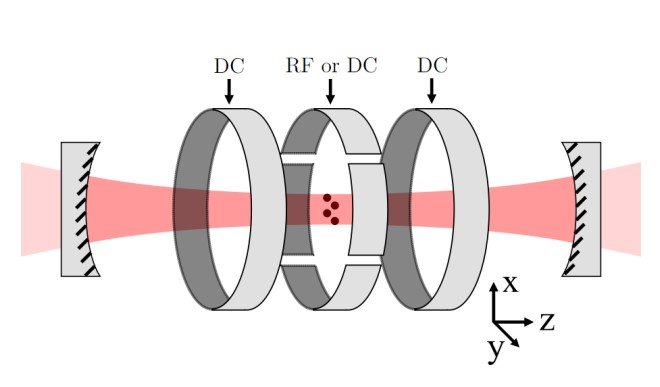
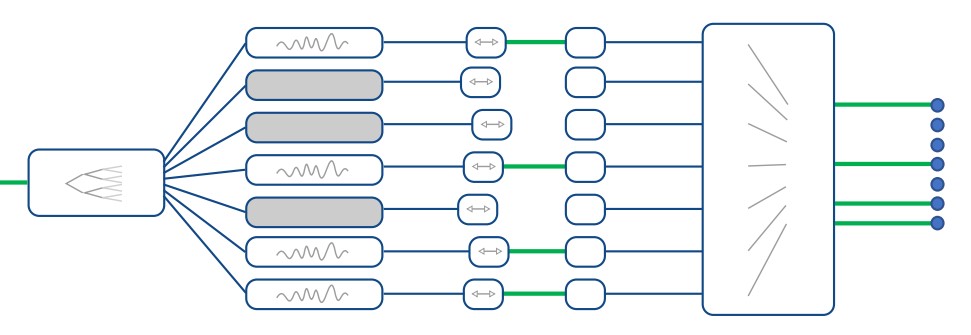
Laser-cooled trapped ions are among the most pristine and controllable quantum systems. Research performed in Prof. Islam’s group is currently focused on the following:
- Quantum simulation: The QITI laboratory is building a programmable trapped-ion quantum simulator with 171Yb+ qubits, with optical controls at the level of individual ions for studying problems in quantum many-body physics and computation.
- QuantumION: In collaboration with Prof. Crystal Senko’s group and supported by Transformative Quantum Technologies (TQT) , we are building QuantumION, a trapped-ion quantum simulator/computer based on a chain of 133Ba+ ions. 133Ba+ is regarded as the ‘Goldilocks qubit’ for their many wonderful properties including long lived metastable states, availability of spin-1/2 hyperfine qubits, and optical transitions in the visible range.
- Quantum simulation algorithms: We research on classical and quantum algorithms to make quantum simulation more efficient, e.g. by using modern machine learning methods. We collaborate with the Perimeter Institute Quantum Intelligence Laboratory
Job opportunities
We acknowledge financial support from University of Waterloo, NSERC, Government of Ontario, US ARO, and Transformative Quantum Technologies (TQT, CFREF).
Recent News
01 Jul 2023 - tenured and promoted
Rajibul is promoted to associate professor with tenure.
Thanks to all the present and past members of the team whose hard work and dedication made this possible!
08 Aug 2022 - Ali defends his MSc thesis!
Congratulations to Ali Binai-Motlagh for successfully defending his MSc thesis on optical addressing for individual Barium qubits! Ali will join Columbia University as a PhD student!
08 Dec 2022 - Darian defends his MSc thesis!
Congratulations to Darian Mclaren for successfully defending his MSc thesis on On the evaluation of quantum instruments with a consideration to measurements in trapped ion systems!
Recent Publications
Investigations of 2D ion crystals in a hybrid optical cavity trap for quantum information processing
Abstract: We numerically investigate a hybrid trapping architecture for 2D ion crystals using static electrode voltages and optical cavity fields for in-plane and out-of-plane confinements, respectively. By studying the stability of 2D crystals against 2D-3D structural phase transitions, we identify the necessary trapping parameters for ytterbium ions. Multiple equilibrium configurations for 2D crystals are possible, and we analyze their stability by estimating potential barriers between them.
Microgram BaCl_2 Ablation Targets for Trapped Ion Experiments
Abstract: Trapped ions for quantum information processing has been an area of intense study due to the extraordinarily high fidelity operations that have been reported experimentally. Specifically, barium trapped ions have been shown to have exceptional state-preparation and measurement (SPAM) fidelities. The 133Ba+ (I=1/2) isotope in particular is a promising candidate for large-scale quantum computing experiments.
A guided light system for agile individual addressing of Ba+ qubits with 1E-4 level intensity crosstalk
Abstract: Trapped ions are one of the leading platforms for quantum information processing, exhibiting the highest gate and measurement fidelities of all contending hardware. In order to realize a universal quantum computer with trapped ions, independent and parallel control over the state of each qubit is necessary. The manipulation of individual qubit states in an ion chain via stimulated Raman transitions generally requires light focused on individual ions.